5 graph problems you should know in Java
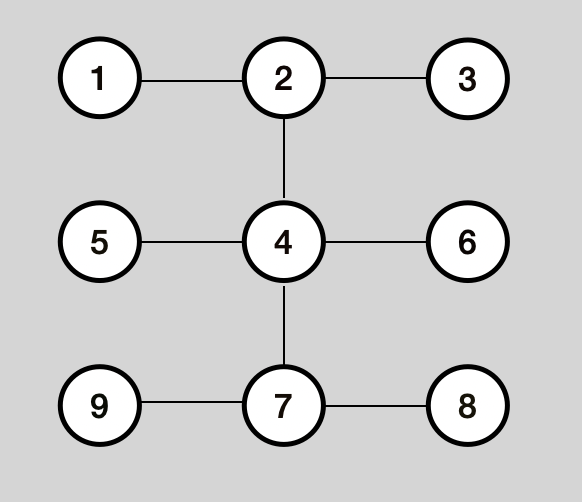
A Graph is a collection of nodes and edges. Graphs are really useful to explain relationships between things, for instance we can represent a map of cities with a graph.
We have directed and undirected graphs. The first type of graphs in order to navigate from node A to node B there must be an edge with a direction from A to B. In undirected graphs if there’s an edge between A and B we can navigate from A to B and from B to A.
How can we implement graph data structure
There are 2 ways of representing a Graph, one is with a adjacency matrix and another way is with an adjacency list. The second one is normaly the way to go and is the most common way to represent a Graph.
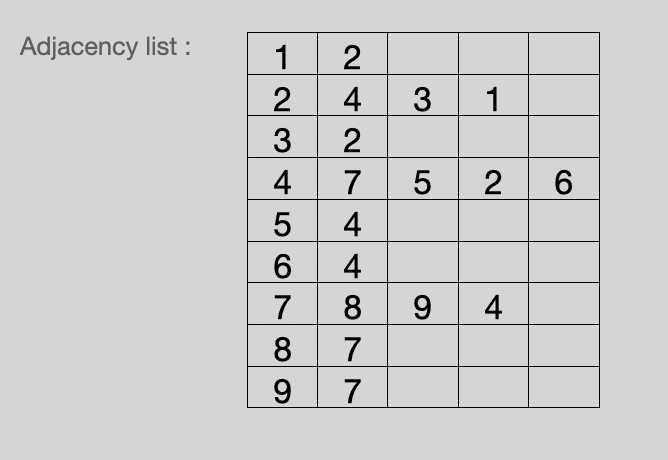
In Java it can be implemented with a Map with keys as nodes and as value the list of nodes that are adjacent to that key. Another way to represent a graph is with LinkedList where each value of this data structure is also a LinkedList with all the nodes adjacent to that node in that position. Even that a node has no neighbours it should appear in the map but with empty value.
Breath first search (BFS)
In this algorithm we traverse the Graph using a Queue. In the course of the traversal every node of the Graph changes it’s state from unvisited to visited. Only when we have visited all the adjacent nodes from the current node we move to the next node.
public class Graph {
private final int V;
private final LinkedList<Integer> adj[];
private final Queue<Integer> queue;
public Graph(int v){
this.V = v;
this.adj = new LinkedList[v];
for (int i=0; i<v; i++){
adj[i] = new LinkedList<>();
}
this.queue = new LinkedList<Integer>();
}
public void addEdge(int v,int w){
this.adj[v].add(w);
}
public void BFS(int n){
boolean visited[] = new boolean[V];
visited[n]=true;
queue.add(n);
while (queue.size() != 0){
n = queue.poll();
System.out.print(n + " ");
for (int a: adj[n]){
if (!visited[a]){
visited[a] = true;
queue.add(a);
}
}
}
}
}
Depth first search (DFS)
In this case we start in a node and we pick a direction and continue in the same direction until we cannot continue. You are exploring one direction as far as you can before switching directions.
This algorithm uses an stack in his iterative version. We have to see as a vertical data structure.
public void DFS(int n){
boolean visited[] = new boolean[V];
Stack<Integer> stack = new Stack<>();
stack.push(n);
while(!stack.empty()) {
n = stack.peek();
stack.pop();
if(visited[n] == false) {
System.out.print(n + " ");
visited[n] = true;
}
for (int a:adj[n]) {
if (!visited[a]){
stack.push(a);
}
}
}
}
Problem 1 - Find if there’s a path between 2 nodes
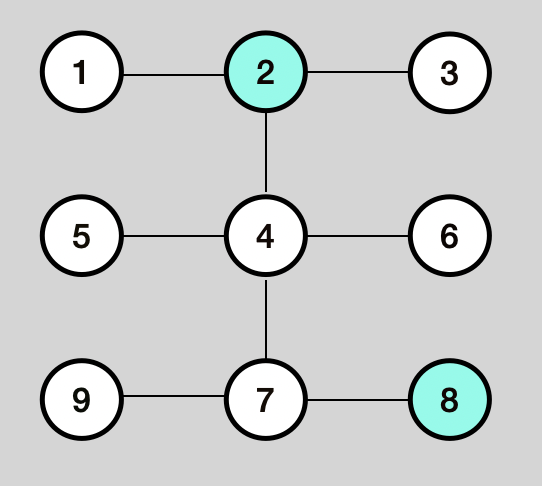
public boolean hasPath(int src, int dest, boolean []visited){
if(visited[node]){
return false;
}
if(src==dst) return true;
visited[node]=true;
for (int neighbor: adj[src]){
if(hasPath(neighbor, dst, visited)){
return true;
}
}
return false;
}
Problem 2 - Count the number of connected components
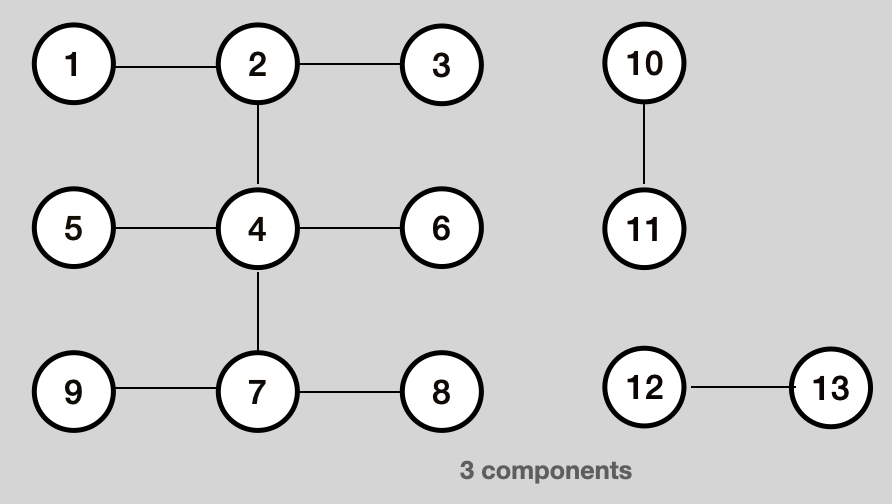
public int connectedComponentsCount(){
boolean visited[] = new boolean[V];
int count = 0;
for (int i = 0; i < V; i++){
if (explore(i, visited)){
count++;
}
}
return count;
}
public boolean explore(int node, boolean visited[]){
if(visited[node]){
return false;
}
visited[node]=true;
for(int neighbor: adj[node]){
explore(graph, neighbor, visited);
}
return true;
}
Problem 3 - Find the largest component
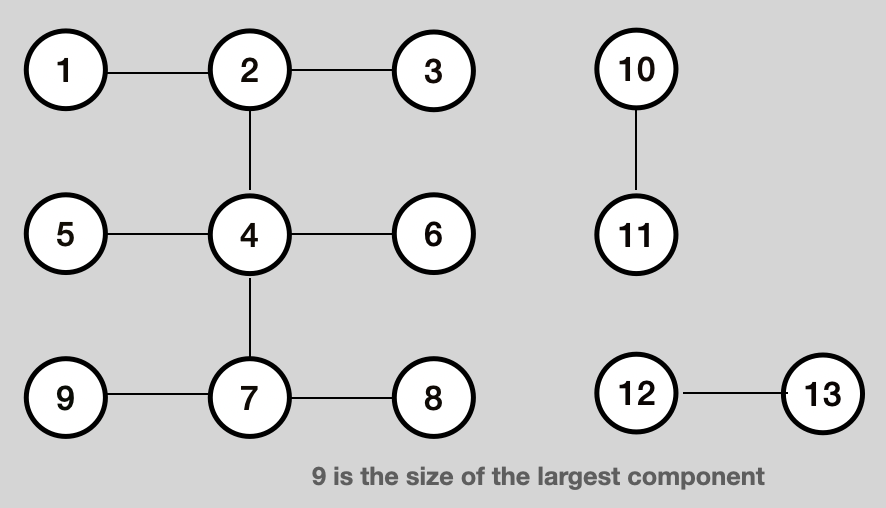
public int largestComponent() {
boolean []visited = new boolean[V];
int largest = 0;
for (int i = 0; i < V; i++) {
int result = exploreSize(i, visited);
if (result > largest) {
largest = result;
}
}
return largest;
}
public int exploreSize(int node, boolean[] visited) {
if (visited[node]) {
return 0;
}
visited[node] = true;
int size = 1;
for (int neighbor : adj[node]) {
size += exploreSize(neighbor, visited);
}
return size;
}
Problem 4 - Find the shortest path between 2 nodes
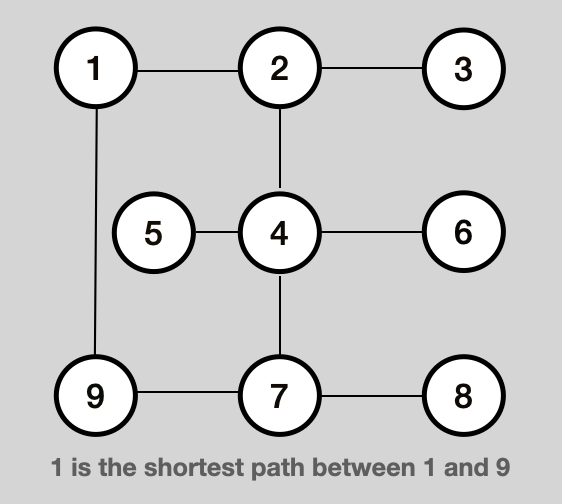
class Node{
int value;
int distance;
}
Queue<Node> queue = new ArrayDeque<>();
public int shortestPath(int src, int dest) {
boolean[] visited = new boolean[V];
visited[src] = true;
queue.add(new Node(src, 0));
while (queue.size() != 0) {
Node node = queue.poll();
if (node.value == dest) {
return node.distance;
}
System.out.print(node.value + " ");
for (int a : adj[node.value]) {
if (!visited[a]) {
visited[a] = true;
queue.add(new Node(a, node.distance + 1));
}
}
}
return -1;
}
public static void main(String args[]) {
Graph g = new Graph(7);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 0);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(2, 3);
g.addEdge(2, 1);
g.addEdge(2, 0);
g.addEdge(3, 2);
g.addEdge(3, 1);
g.addEdge(3, 4);
g.addEdge(4, 3);
g.addEdge(5, 6);
g.addEdge(6, 5);
System.out.println("Shortest path: " + g.shortestPath(4, 0));
}
Problem 5 - Count the number of islands
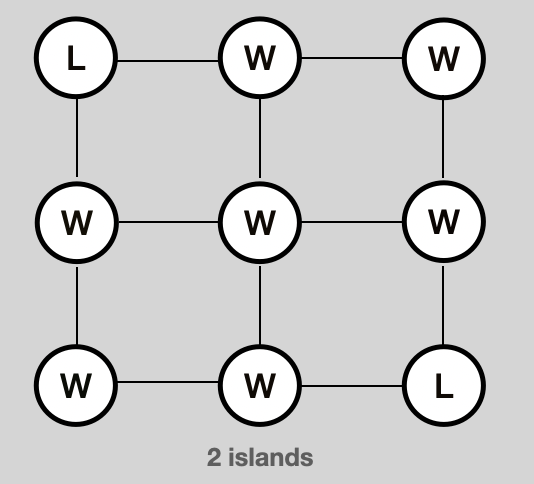
public class IslandCounter {
public int countIslands(char[][] grid) {
boolean[][] visited = new boolean[grid.length][grid[0].length];
int islands = 0;
for (int row = 0; row < grid.length; row++) {
for (int column = 0; column < grid[0].length; column++) {
if (explore(grid, row, column, visited)) {
islands++;
}
}
}
return islands;
}
public boolean explore(char[][] grid, int row, int column, boolean[][] visited) {
boolean rowInbounds = 0 <= row && row < grid.length;
boolean columnInbounds = 0 <= column && column < grid[0].length;
if (!rowInbounds || !columnInbounds) return false;
if (visited[row][column]) return false;
if (grid[row][column] == 'W') return false;
visited[row][column] = true;
explore(grid, row - 1, column, visited);
explore(grid, row + 1, column, visited);
explore(grid, row, column - 1, visited);
explore(grid, row, column + 1, visited);
return true;
}
public static void main(String[] args) {
IslandCounter islandCounter = new IslandCounter();
char [][] grid = { {'L','L', 'W','W', 'L'}
,{'L','L', 'W','W', 'W'}
,{'W','W', 'W','W', 'W'}
,{'W','W', 'W','L', 'L'}
,{'L','W', 'W','L', 'L'}};
System.out.println("Number of islands in this grid :" +islandCounter.countIslands(grid));
}
}
Conclusion
In this post we have seen how to define a graph data structure in Java. We have seen 5 problems related with graphs and how to implement them using Java. We have seen 2 key algorithms that help us solve this kind of problems, DFS and BFS.

Comments