Set zeroes in a matrix algorithm in Java

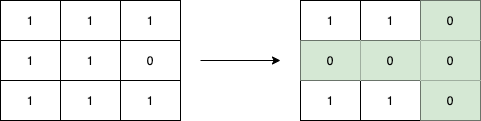
In this post we are going to see a solution to solve the following leetcode problem https://leetcode.com/problems/set-matrix-zeroes/

In this problem if there’s a 0 in a position of a MxN matrix we have to set all the values of the row and the column where this 0 appears changing 1’s for 0’s.

The first approach

One option could be using extra space creating another matrix of MxN where when we find a 0 in the input matrix we set all the values of the row and column to 0 in the extra matrix and when we have traversed all the input matrix copy back all the values in the input matrix. Space complexity is O(M*N) because we are allocating extra space.

Using constant space

A better approach is to use the same input matrix to mark the row and/or column that has to be converted to 0’s. For this we can mark the first position of the row and the first value of the column while we are traversing the input matrix to know the state of that row/column. This way in the second matrix traversal if the first position of the row or the first position of the column is 0 we can set the current value that we are visiting to 0.

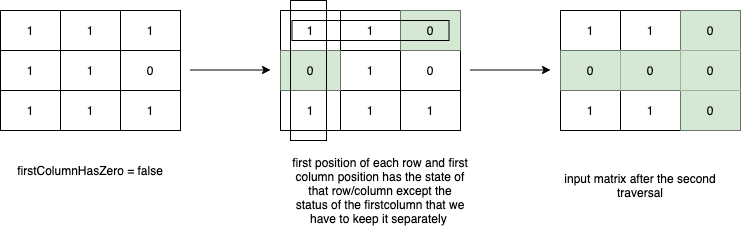
We have to consider that in the first column of the matrix we would have the state of each row in the matrix and the state of the first column, so we can use an extra boolean to know the status of the first column (if there’s any 0) and use the first position of each row to store the state of that row in the matrix.

The code

class Solution {
    public void setZeroes(int[][] matrix) {
        int rows = matrix.length; 
        int cols = matrix[0].length;
        boolean firstColumHasZero = false;
        
        for(int i=0; i<rows; i++){
            if(matrix[i][0]==0){
                firstColumHasZero = true;
            }
            for(int j=1; j<cols; j++){
                if(matrix[i][j] == 0){
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }     
        for(int i=rows-1; i>=0; i--){
            for(int j=cols-1; j>=1; j--){
                if(matrix[i][0]==0 || matrix[0][j]==0){
                    matrix[i][j] = 0;
                }
            }
            if (firstColumnHasZero) {
                matrix[i][0] = 0;
            }
        }
    }
}

Conclusion

This problem has time complexity O(MxN) because we have to interate over all the matrix, and O(1) space complexity because we are not allocating extra space.